Die MESYS Wellensystemberechnung erlaubt seit 2016 den Import von 3D-Gehäusen als 3D-STEP Dateien. Die Software vernetzt die Bauteile automatisch und generiert die reduzierten Steifigkeitsmatrizen, die zuvor in separaten FE-Berechnungen bestimmt werden mussten und dann importiert werden konnten.
Mit Version 04/2017 wird die Integration von 3D-elastischen Bauteilen in der MESYS Wellensystemberechnung weiter ausgebaut. 3D-elastische Gehäuse können nicht nur in einer statischen Berechnung berücksichtigt werden, sondern über eine modale Reduktion auch in der Berechnung von Eigenfrequenzen. Der Einfluss von elastischen Gehäusen auf die Eigenfrequenzen ist dabei deutlich grösser als auf die statischen Deformationen.
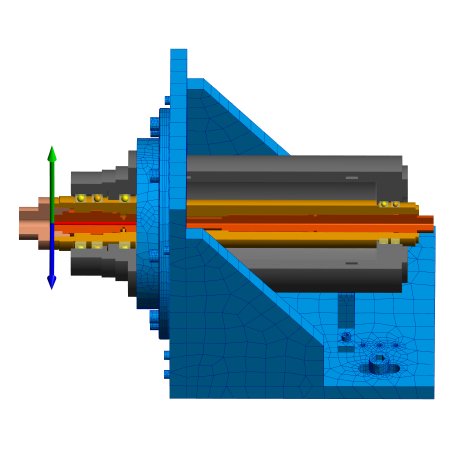
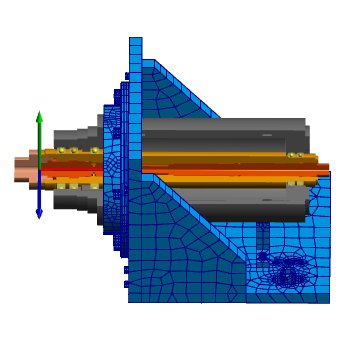
Beispielsweise ergibt sich für einen L-förmigen Spindelprüfstand ohne die hintere Stütze der Spindel und ohne Gehäusesteifigkeiten eine erste axiale Eigenfrequenz von knapp 22'000 1/min. Mit Steifigkeitseinfluss des Gehäuses ist die erste Eigenfrequenz eine Biegeeigenfrequenz von knapp 15’200 1/min, was bei einer vorgesehenen Betriebsdrehzahl von 15’000 1/min zu Problemen führen würde. Mit der hinteren Stütze steigen die Biegeeigenfrequenzen auf 25'000 1/min, die erste axiale Eigenfrequenz reduziert sich auf 19'600. Das importierte CAD-Modell war das bestehende CAD-Modell für die Fertigung. Dies ist mit den diversen Bohrungen nicht optimal, kann aber dennoch verwendet werden kann. Eliminiert man die Bohrungen im CAD-Modell würde sich der Speicherbedarf und die initiale Rechenzeit für die Berechnung reduzieren.
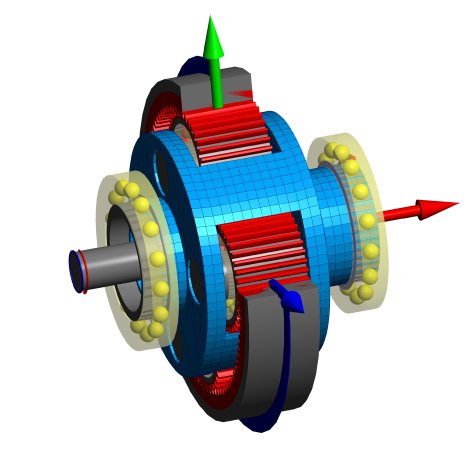
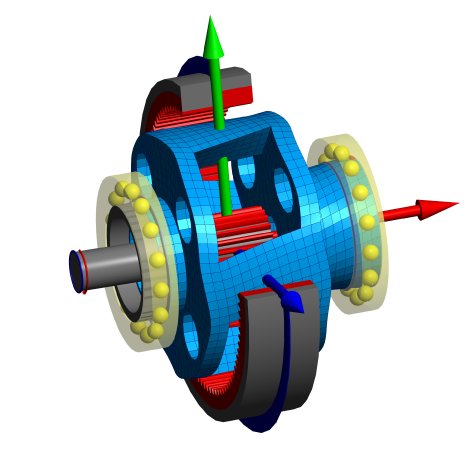
Eine weitere Ergänzung ist die Unterstützung von 3D-elastischen Planetenträgern. Im Unterschied zu Gehäusen rotieren Planetenträger im System und daher muss die Berechnung mit den entstehenden grossen Rotationen umgehen können. Die elastischen Deformationen des Planetenträgers haben Einfluss auf die Lastverteilung der Verzahnungen und sind daher wichtig für die Auslegung von Verzahnungskorrekturen. Die Verkippung der Planeten beeinflusst auch die Lagerbelastungen sowie die globale Verdrehsteifigkeit.
Planetenträger können als CAD-Modell eingelesen werden oder mit Parametern definiert werden. Für die parametrischen Planetenträger stehen vier Varianten zur Verfügung.
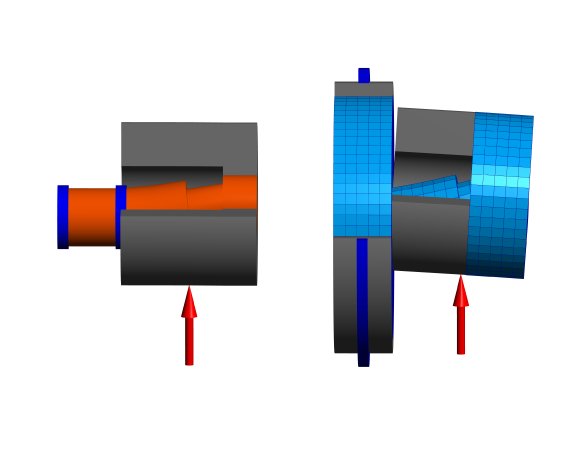
Eine weitere Möglichkeit einer Integration von 3D-elastischen Bauteilen in die Wellenberechnung ist die Nutzung von rotationssymmetrischen 3D-Wellen, die über einen Polygonzug definiert werden können. Diese 3D-elastischen Bauteile definieren eine zusätzliche Steifigkeitsmatrix. Als Beispiel für den Einfluss auf die Berechnung wird hier ein Flexpin betrachtet. In der älteren Literatur angegebene Gleichungen für die Deformation eines Flexpins basieren oft auf einem Euler-Bernoulli-Balken ohne Berücksichtigung von Schubverformungen. Bei einem Beispiel ergeben sich bei einem Balkenmodell ohne Schubverformungen eine Durchbiegung von 15µm, mit Schubverformungen 23µm und bei Verwendung von 3D-elastischen Bauteilen 42µm. Mit dem 3D-elastische Bauteil ergibt sich also eine um über 80% grössere Durchbiegung gegenüber einer Berechnung mit einem schubelastischen Balkenelement. Der Grund sind die Deformationen in den zwei Pressverbänden; eine starre Kopplung der Balkenelemente ist zu steif. Das 3D-elastische Bauteil bildet die Deformationen im Pressverband besser ab. Da ein quasi-verschweisstes Bauteil in der Berechnung betrachtet wird, wird die reale Durchbiegung noch etwas grösser werden, da es zu Schlupf im Pressverband kommen kann.
Die Integration von 3D elastischen Bauteilen in die Wellensystemberechnung erlaubt eine Berücksichtigung von zusätzlichen Steifigkeiten, ohne dass externe FE-Programme benötigt werden. Eine zeitaufwändige und fehleranfällige Übernahme von Steifigkeitsmatrizen entfällt daher.
Eine vollständige Berechnung in FE-Programmen bietet mehr Freiheiten in Bezug auf die Wahl von Randbedingungen und erlaubt nichtlineare Berechnungen mit Kontakt. Die Wellensystemberechnung auf Basis von eindimensionalen Elementen bietet aber den wesentlichen Vorteil von schnellen Rechenzeiten im Sekundenbereich, die umfangreiche Lastkollektivberechnungen und Parametervariationen erst möglich machen. Mit der Integration von 3D elastischen Bauteilen bleiben diese Vorteile erhalten.